转自科学网张召富
当半导体/半导体,或者绝缘体/半导体接触形成界面结构时, 因为禁带宽度不同,在两侧材料的导带底和价带顶处会形成不连续的台阶,即能带台阶 (band offset),其中导带底处的能带台阶被称为导带台阶 (conduction band offset, CBO),价带顶处的能带台阶被称为价带台阶(valence band offset, VBO)。视能带对其情况不同,半导体异质结被分为三类:type-I, type-II, 和 type-III,其能带图如图1[1]:

▲图1 The three types of semiconductor heterojunctions organized by band alignment.
半导体能带对齐有重要意义。比如,对于电子器件来说,常用的为 type-I band alignment, 要求 CBO/VBO 大于 1eV 才能更有效的束缚电子/空穴,减小漏电[2]。type-II 异质结在异质结光催化分解水领域,可以有效减小电子空穴对符合,提高光催化效率[3]。
界面两侧的能带对齐(band alignment)依赖于两侧材料的电荷转移。当异质结两侧无电荷转移时候,CBO 是由异质结两侧材料的电子亲和势 (electron affinity, EA) 决定,被称为electron affinity model,又称为 Anderson's rule[4]。
在这个模型中,认为两侧真空能级持平,根据两侧材料的 EA 不同,得到两侧材料的 CB 位置,即 CBO。根据材料的禁带宽度 Eg 数值,即可得到价带的相对关系,即 VBO。另外的办法是采用一个外来的参考能级做参考标准,比如采取过渡金属杂质的高度局域化的 d 轨道能级来做参考标准[5] ,或者采用材料中 H 的 (+/-) 能级来做参考标准[6]。
实际的界面中,通常存在电荷转移,形成界面 dipole。界面 dipole 会调整 band alignment, 使得 band alignment 不再遵循 electron affinity model。描述有电荷转移的异质结的物理模型有多个,其中常用的 CNL 模型表达式为[2]

其中 χ 为 electron affinity,ɸCNL charge neutrality level (CNL) 是半导体能带结构中的一个参考能级,由材料性质(能带结构)来决定。
S 为 Fermi-level pinning factor,表征半导体材料的 Fermi-level pinning 特点的:S=1 表征无 pinning 的 Schottky limit;S=0 表征强 pinning 的 Bardeen limit。对于半导体异质结来说,S 通常由 Eg 更大的一侧来决定。对很多半导体材料比如 Si 来说,S 值比较小,上述公式第三项可以忽略,即在强 pinning 情况下,能带对齐由两侧材料的 CNL 的对齐来确定。
而 CNL 与真空能级能量差可以表征半导体材料的电负性,即上述公式表示,半导体异质结的能带对齐是考虑 S 因子屏蔽作用下异质结两侧材料的电负性之差。对 CNL 模型的更详细讨论可以参考[2]。这里暂不对其他讨论半导体异质结能带对齐的物理模型展开详细描述,有兴趣的可以参考 [7-8]以及更多的相关文章。
在材料计算中,可以通过建立半导体异质结界面模型,进行第一性原理计算得到。关于半导体异质结界面建模方法等有时间再单独开贴介绍。注意,不建立界面模型也可以计算材料的 band alignment,但是必须要求一个参考能级来进行 line-up。即便如此,这样求解出来的 band alignment 并没有考虑到电荷转移的效果。
界面模型中如何得到 band alignment, 有多个办法。其中较为常见的为:local DOS (LDOS, or partial DOS, PDOS) method、core-level alignment method, 和 averaged potential alignment method。通过分析计算数据便可得到 VBO, 而获取 CBO 办法,可以根据公式 CBO=Eg1-Eg2-VBO 得到。结合论文(介绍前两个method的图来自我的论文,欢迎引用),逐一介绍如下:
(1)LDOS (or PDOS) method
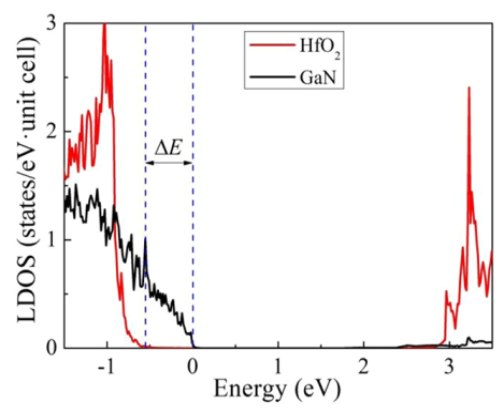
▲图2 LDOS method to get the band alignment at HfO2/GaN interface.[9]
以上图为作者发表的论文 HfO2/GaN 界面模型为例[9]介绍。首先建立异质结界面模型(见表面界面建模要点/经验小结 Summary about surface/interface modeling),然后对弛豫的界面模型进行 DOS 计算。取界面两侧远离界面的GaN原子和 HfO2 原子(也可以分别取Ga原子N原子Hf原子O原子)画出其PDOS,这时得到的价带顶能量之差即为 VBO。
该方法原理为:远离界面的原子可以较少受到 interface interaction,即基本上保持其 bulk behavior;认为在界面超胞模型中两侧材料的真空能级是持平的,所以得到的价带顶能量之差即为界面的 VBO。而获取 CBO 办法,可以根据公式 CBO=Eg1-Eg2-VBO 得到。
注意:1.如果是用计算的 Eg 值则必须考虑DFT计算引入的低估禁带的问题,即采用杂化泛函计算;也可以考虑直接取实验 Eg 值。2. 如果是用该方法来比较不同模型中 BO 变化趋势是足够的,如果是为了直接得到具体值,会存在一定误差。
(2)Core-level alignment method
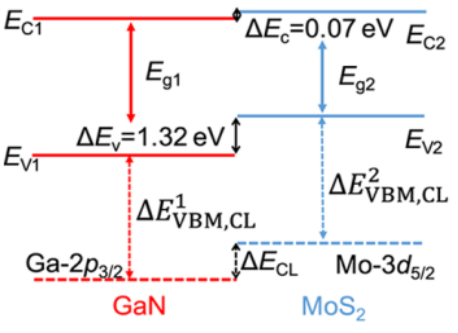
▲图3 Core level alignment method to get the band alignment at MoS2/GaN interface.[10]
以上图我发表的论文MoS2/GaN界面模型为例[10]介绍。这个方法的原理是:认为无论在界面材料还是体材料中,材料的价带顶与芯能级能量之差是定值。核外电子分为价电子和芯电子(valence electrons and core electrons),其中 core electron 与 core state 被认为是稳定的态,不被成键等来影响。实验角度,芯能级可以通过 XPS 表征方法得到,所以根据这个办法,既可以用于实验研究异质结能带对齐,也可以通过计算来讨论。上图是我用实验 XPS 方法得到的 MoS2/GaN 异质结能带对齐结果。在文献[10]跟[11]中我也从计算角度提取了MoS2/GaN 以及 SiNx/GaN 的能带对齐,跟实验值较相近。
基于该方法做计算(或者实验)讨论的具体做法:1. 计算体材料A(与体材料B)的芯能级,读取出芯能级跟价带顶能量差ΔEA (ΔEB);2. 提取界面模型两侧远离界面区域的原子的芯能级Ecore-A (Ecore-B);3. Ecore-A+ ΔEA 与 Ecore-B+ ΔEB 则为异质结两侧 AB 材料各自的价带顶,其能量差则为 VBO。该方法准确性更高,并且可以与实验结合,被很多人采用。推荐几篇用 core level 的很经典的文献[12]。
至于如何从计算角度获取芯能级信息,可以考虑两个方法:a. VASP 计算 INCAR 中加入ICORELEVEL=1 即可在 OUTCAR 中输出每一个原子的芯能级芯能级信息。b. 直接考虑在dos 或者 band 图中读出最深的一个 band (or PDOS)的能量位置作为 core level (or semi-core level)。
(3)Averaged potential alignment method
该方法我暂时还未用过。其原理跟 core-level method 接近,认为无论在界面材料还是体材料中,材料的价带顶与平均静电势能量之差是定值。该方法的做法为:
1. 得到体材料 A(体材料 B)的 planar-averaged electrostatic potential;
2. 对其再做平均得到 macroscopic-averaged electrostatic potential,读出该 potential 跟价带顶能量差 ΔEA (ΔEB);
3. 提取界面模型两侧远离界面区域的几个原子层,读取出其 macroscopic-averaged electrostatic potential 分别为 EA (EB);
4. EA+ ΔEA与EB+ ΔEB 则为异质结两侧AB材料各自的价带顶,其能量差则为 VBO。
很容易看出,该方法跟 core-level 方法很类似。其优点是可以借助 average potential 讨论charge transfer,但是缺点是 averaged potential 这个概念是纯物理的概念,实验的参考性较低。推荐几篇用 averaged potential alignment 的很经典的文献比如[13]。
补充一个漏掉的可以进行粗略进行能带对齐的方法,common-anion rule: compound semiconductors which have the same anion will form an interface with near zero valence-band discontinuity [14]
[1] https://en.wikipedia.org/wiki/Heterojunction
[2] J. Robertson, J. Vac. Sci. Technol. B 18, 1785 (2000); J. Robertson, J. Vac. Sci. Technol. A, 31, 050821 (2013); J. Robertson, Journal of Applied Physics 100, 014111 (2006);
[3] R. Marschall, Adv. Funct. Mater. 2014, 24, 2421–2440
[4] R. L. Andersen, Solid-State Electron. 5, 341 (1962).
[5] M. J. Caldas, A. Fazzio, and Alex Zunger, Appl. Phys. Lett. 45, 671 (1984).
[6] C. G. Van de Walle, and J. Neugebauer, Nature 423, 626–628 (2003)
[7] J. O. McCaldin,T. C. McGill, and C. A. Mead, Phys. Rev. Lett. 36, 56 (1976)
[8] R. T. Tung, Phys. Rev. Lett. 84, 6078 (2000); R. T. Tung, Phys. Rev. B 64, 205310 (2001)
[9] Zhaofu Zhang, et al, ACS Appl. Mater. Interfaces 2015, 7, 5141−5149
[10] Zhaofu Zhang, et al, ACS Appl. Mater. Interfaces 2018, 10, 17419−17426
[11] Zhaofu Zhang et al, Appl. Phys. Express 11 081003 (2018)
[12] S. P. Kowalczyk, et al, Phys. Rev. Lett. 44, 1620 (1980); Su-Huai Wei and Alex Zunger, Appl. Phys. Lett. 72, 2011 (1998); Su-Huai Wei, et al, Appl. Phys. Lett. 94, 212109 (2009)
[13] C. G. Van de Walle and R. M. Martin, Phys. Rev. B 34, 5621 (1986); A. Baldereschi, S. Baroni, and R. Resta, Phys. Rev. Lett. 61, 734 (1988); Alfredo Pasquarello, et al, Appl. Phys. Lett. 107, 211601 (2015)
[14] J. O. McCaldin, T. C. McGill, and C. A. Mead Phys. Rev. Lett. 36, 56 (1976); Kowalczyk, S. P.; Cheung, J. T.; Kraut, E. A.; Grant, R. W. Phys. Rev. Lett. 56, 1605 (1986).

